论文
《A Monocular SLAM System Leveraging Structural Regularity in Manhattan World》(2018ICRA,Wuhan University,China)
开源代码
项目主页:包含本文中三个创新点对应的代码,基于灭点的旋转矩阵的优化(Matlab代码)、基于共面的平移向量优化(Matlab代码)、三维地图的优化(C++,使用Ceres库)。
实验室
武汉大学遥感与信息工程学院
Motivation & Background
- 将基于特征的SLAM分为结构性的和非结构性的;
- 非结构性的vSLAM(包括非结构性性的点和线特征)存在问题,对于点:纹理稀疏的问题;对于线:提取和遮挡的问题;
- 在曼哈顿世界中,结构性表示为两个方面:
- 以灭点为代表的平行垂直关系:同一主方向的三维线段互相平行、不同主方向的三维线段互相垂直。已有的利用这类结构性的SLAM系统存在问题:当无法获得视觉之外传感器的数据时,这些系统的鲁棒性会受较大影响;基于灭点的方法只能减小旋转运动的误差,对减小平移误差贡献不大。
- 场景中部分点线特征具有共面约束,这些平面的法向量与Manhattan场景中的主方向平行。有学者尝试利用共面约束,但是他们没有利用Manhattan场景中平面法向量固定的先验知识,系统不够鲁棒。
上述两类Manhattan结构性中,利用第二类共面约束的工作:
- 《Efficient homography- based tracking and 3-D reconstruction for single-viewpoint sensors》(2008 IEEETransOnRobotics)[11]
- 《Monocular SLAM with locally planar landmarks via geometric Rao-Blackwellized particle filtering on Lie groups》(CVPR2010)[12]
- 《Extraction, matching, and pose recovery based on dominant rectangular structures》(CVIU2005)[13]
Contribution
- 提出了一个新的利用平行垂直约束的旋转矩阵优化策略;
- 一个新的利用共面约束的平移向量优化策略;
- 基于平行、垂直、共面约束的高效三维地图优化策略。
Content
文中提出的系统先使用已有的方法来估计出相机位姿和三维地图(《PL-SLAM: Real-time monocular visual SLAM with points and lines》[6]中的方法),然后使用提出的基于平行、垂直、共面约束的优化策略来对估计出的相机位姿和三维地图进行进一步的优化。
几何约束的数学表示
Manhattan世界的三个主方向表示为(世界坐标系下):
\[D=\{d_k\}_{k=1}^3\]总的来说,三维线段间的平行、垂直约束主要以灭点形式表示,三维点和三维线段的共面约束主要以单应矩阵形式表示。
平行、垂直约束
这部分参考《Multiple View Geometry》8.6节。
在第 $i$ 帧中,三个主方向分别对应一个灭点:
\[V_i=\{v_k^i\}_{k=1}^3\]灭点与主方向的关系(其中 $K$ 和 $R_i$ 分别为相机的本质矩阵、第 $i$ 帧的旋转矩阵, $\varpropto$ 表示忽略尺度情况下的相等):
\[v_k^i \varpropto KR_id_k\]同时灭点与相机光心的连线(灭点方向VD: $\delta$ )与当前帧坐标系下的灭点方向的三维直线平行:
\[\delta_k^i \varpropto d_k^i \varpropto R_id_k\]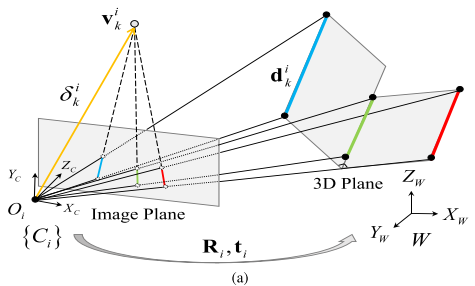
共面约束
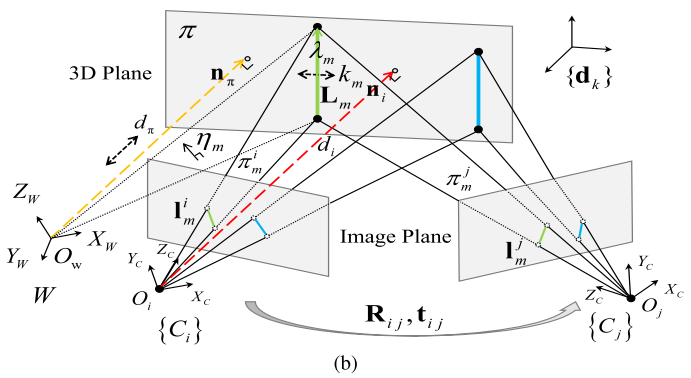
同一平面 $\pi$ 内的三维线段集合表示为:
\[\mathcal{L} = \{L_m\}_{m=1}^M\]$\mathcal{L}$ 投影到第 $i$ 帧和第 $j$ 帧,两帧中的共面投影线段匹配对表示为:
\[\mathcal{M} = \{l_m^i,l_m^j\}_{m=1}^M\]由于这些投影线段属于同一个三维平面,因此这些线上的点在两帧之间的转换满足同一个单应矩阵 $H_{ij}$ ,假设 $p_m^i$ 为线段 $l_m^i$ 上的点,则有:
\[{l_m^j}^TH_{ij}p_m^i = 0\]对于共面点,有:
\[p_n^j \varpropto H_{ij}p_n^i\]共面线段的约束图示:
旋转矩阵的优化
分为以下几个步骤:
- 灭点提取,使用《Globally optimal line clustering and vanishing point estimation in Manhattan world》(2012CVPR)[15]论文中的方法。然后使用上述灭点和主方向之间的转换关系,得到Manhattan场景下的三个主方向。
- 利用全局绑定(Global Binding)优化相机绝对位姿中的旋转矩阵,构造目标函数如下(利用VD与三维线段的平行约束): \(E(\omega_i) = \sum_{k=1}^{3}E_k(\omega_i) = \sum_{k=1}^{3}arccos(\delta_k^iR_id_k)\)
- 基于相对位姿优化优化相机绝对位姿中的旋转矩阵,由 $\delta_k^j \varpropto R_{ij}\delta_k^i$ 可得: \([\delta_k^j]_{\times}R_{ij}\delta_k^i = 0\)
以上优化步骤中更新的都是相机绝对位姿中的旋转矩阵 ${R_i}$ 。
平移向量的优化
- 确定共面特征(线+点)。首先利用在两帧中找到的同向线段集合(对应三个主方向,每帧三个同向线段集合),确定两帧间共面线段的候选集合(这些集合中的线段都是互相平行的,但不一定共面),然后使用《Planar structures from line correspon- dences in a manhattan world》(2015ACCV)[19]中的方法,利用Characteristic Line(CL)参数表示来获取共面线段匹配 ${\mathcal{M_u}}$,基于 ${\mathcal{M_u}}$ 得到两帧间此平面对应的单应矩阵,由此计算出共面点特征匹配 ${\mathcal{P_u}}$。
- 构造优化过程中的目标函数,这里的核心有两个:一个是利用前面所述的共面点和线之间的单应矩阵约束;二是将单应矩阵表达形式进行分解(参考《多视几何》,其中 $d_i$ 为相机光心到平面 $\pi$ 之间的距离, $t_{ij}$ 为两帧之间的平移向量): \(H_{ij} = K(R_{ij}+\frac{t_{ij}}{d_i}{n_i}^T)K^{-1}\)
按照之前描述的基于单应矩阵的共面约束的表达形式,可以分别构造共面点和共面线的误差函数,然后基于此进行优化。
三维结构的优化
这里基于上述平行、垂直、共面约束对三维线特征进行优化。此处使用Plucker坐标来表示三维线段:
\[u_m = [\eta_m,\lambda_m]\]其中两个参数,一个为线矩、一个为线方向( $\lambda_m$ ),平面表示为:
\[\pi = [n_{\pi},d_{\pi}]\]其中两个参数,一个为平面法向量,一个为相机光心到平面的距离( $d_{\pi}$ )。
在整个优化过程中,基于共面约束,固定 $\lambda_m$ 和 $n_{\pi}$ ,即未知参数为 $\eta_m$ 和 $d_{\pi}$ ,又由于共面约束 $u_m\pi = 0$ , $\eta_m$ 中仅存在一个未知参数 $k_m$ ,利用投影误差函数对以上两个未知参数进行优化。
Experiments
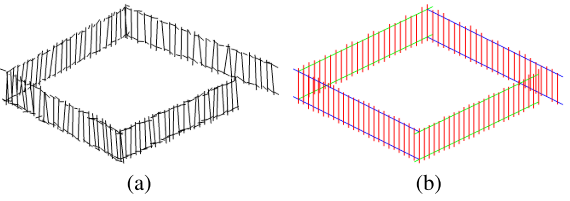
在模拟场景下的建图效果,a图为《Real-time monocular SLAM with straight lines》(2006BMVC)的结果,b图为本文系统建图效果:
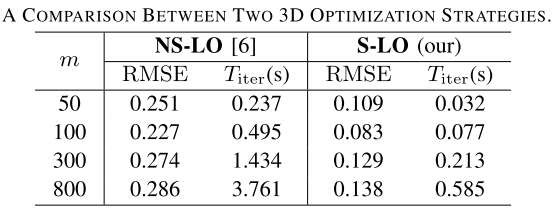
模拟数据集上的位姿优化精度见下图,其中m为三维线段数目,NL-LO表示《PL-SLAM: Real-time monocular visual SLAM with points and lines》论文中的系统
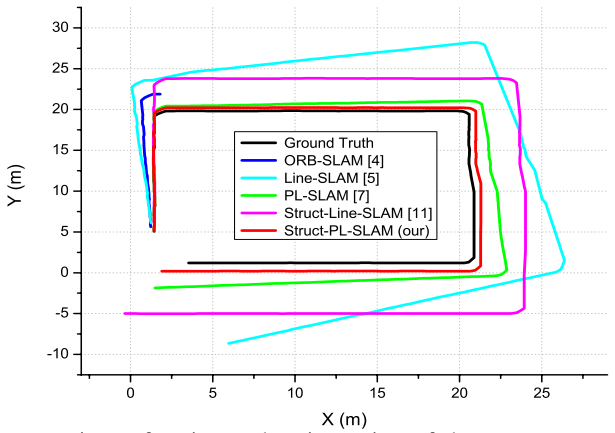
在HRBB4数据集上的相机位姿轨迹:
Conclusion
这篇文章给出了基于平行、共面约束的线特征优化方法,并且给出了相应代码,个人看来,其主要贡献在于已知共面特征、共线特征后如何使用这个约束对位姿及三维地图进行优化,文章描述清楚了基于灭点和单应矩阵的优化方式。但对于整个SLAM系统而言,还有不少欠缺的拼图。(另外本人对文中三维结构优化过程的fix操作还有些疑问,待代码阅读之后更新)
转载请注明原地址,魏鑫燏的博客: http://slowlythinking.github.io 谢谢!





