论文
《StructSLAM : Visual SLAM with Building Structure Lines》(2015IEEE Transactions on Vehicular Technology, Shanghai Jiao Tong University)
Open Source
None.
BackGround
Manhattan World Assumption
曼哈顿世界假设,用于描述人造场景中结构规整性(structural regularity)的一部分,即多数人造场景中的平面都包含着三个相互垂直的主方向。
这个假设来自论文《Manhattan world: Compass direction from a single image by bayesian inference》(1999 ICCV),这篇文章是为了从单幅图像中检测拍摄该图像的相机的朝向(仅水平方向信息),目的是为视障人士提供导航帮助(20年过去了,目前这个基于视觉的应用似乎还未能实现)。论文中对曼哈顿世界假设的表述:
Most indoor and outdoor city scenes are based on a cartesian coordinate system which we can refer to as a Manhattan grid. This grid defi nes an $\vec{i}$; $\vec{j}$; $\vec{k}$ coordinate system.
传统线特征SLAM的问题
由于图像中的线特征存在局部遮挡、端点难以准确定位等问题,线特征比点特征更加难以跟踪,这也导致了线特征SLAM不太出名。
在论文《Vpass: Algorithmic compass using vanishing points in indoor environments》(2009IROS)中,室内环境下,灭点被当做一个全局特征,提升了SLAM的性能。
在论文《Loop closure through vanishing points in a line-based monocular slam》(2012 IEEE PRA)中,作者使用垂直线段和地板平面的线段作为SLAM中的特征,来解决3自由度的位姿跟踪问题,同时使用灭点来减小累积误差、实现闭环检测。
以上两篇论文证明了人造场景中结构规整的特性能够提升SLAM的性能,是本文的Motivation之一。
Motivation
目前视觉SLAM的问题:
- 在纹理稀疏的场景中常见的点特征SLAM效果不好。
- 视觉SLAM存在误差累积,如果不使用闭环检测等方法,误差会越来越大。
- 线特征可以成为点特征的一个良好补充。
- 目前基于线特征的SLAM在性能上并没有明显进展,这是因为对线特征进行鲁棒跟踪比较困难。
以上问题可以从人造场景的曼哈顿假设出发,寻求特殊的线,解决误差累积、线特征难以跟踪等问题。
Contribution
提出了Structure Line Feature,包括它的参数表示方法,通过Structure Line对相机位姿中方向参数的全局约束,提高了视觉SLAM在人造建筑场景中的稳定性和准确度。
Content
Structure Line的参数表示形式
Structure Line:沿着曼哈顿世界假设中三个主方向的直线
参数表示:见下图。其中蓝色直线$l$为Structure Line,$\eta$为曼哈顿世界假设中的一个主方向,$A$是参数平面$XZ$与$l$的交点,$A$周围的阴影表示$l$在参数平面的协方差,参数平面的选取基于$l$与平面法向量的夹角,夹角最小的作为参数平面,$XYZ$为世界坐标系,$O$是相机光心,$O’$ 是光心投影到参数平面的点。
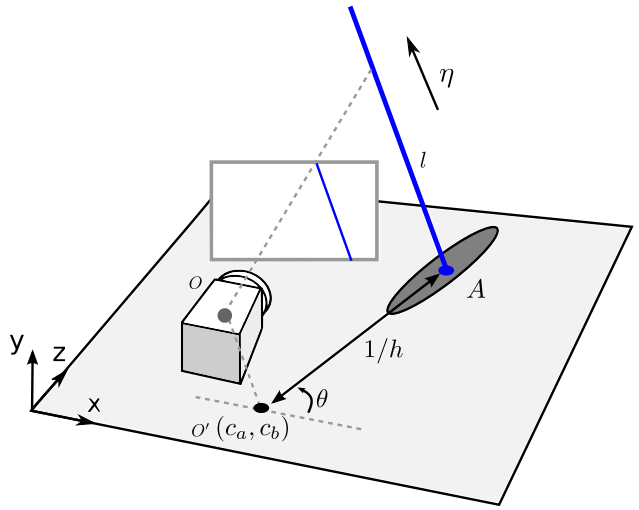
总结,Structure Line表示为(其中$h$表示逆深度):
\[l=(c_a,c_b,\theta,h)\]StructSLAM框架
使用基于EKF的SLAM框架,近似于《Real-time simultaneous localisation and mapping with a single camera》(2003ICCV)论文中的框架。
数学表示:
- 相机状态表示:$x_c$
- 特征点:$x_p=[m_1^T,m_2^T,…]^T$(论文中说$m\in\mathbb{R}^{6\times1}$,不明白多的三个维度是什么)
- Structure Line:$x_l=[l_1^T,l_2^T,…]^T$
- 协方差矩阵: \(\begin{bmatrix} \Sigma_{cc} & \Sigma_{cp} & \Sigma_{cl} \\ \Sigma_{pc} & \Sigma_{pp} & \Sigma_{pl} \\ \Sigma_{lc} & \Sigma_{lp} & \Sigma_{ll} \end{bmatrix}\)
曼哈顿场景主方向分析
在Structure Line初始化之前,必须确定三个主方向,这个过程可以通过将图像中的灭点$v$重投影到三维世界坐标系下来实现。图像中灭点的检测:灭点是图像中平行线(三维空间中平行)的交点,当检测出图像中的平行线之后,就可以计算灭点了。
图像中平行线(三维空间中平行)$s$的检测:使用J-linkage方法,此方法在以下论文中被采用:
- 《Robust multiple structures estimation with j-linkage》(ECCV2008 代码)
- 《Non-iterative approach for fast and accurate vanishing point detection》(ICCV2009 代码)
当平行线$s$检测出来之后,灭点$v$可这样计算:$s^Tv=0$,然后对$s$进行优化,使用非线性最小二乘优化方法,其代价函数为观测线段端点到直线(由灭点和观测线段中点确定)的距离。
由灭点计算主方向是一个灭点的重投影过程,当计算出两个主方向之后,第三个主方向也可以得到(三个方向互相垂直)。
\[\eta \varpropto \mathbf{R}^{wc}\mathbf{K}^{-1}v\]在主方向计算结束后,可以根据上述公式的等价形式把主方向再投影回图像,计算通过平行线与投影点的关系来对主方向进行优化。
Structure Line的初始化
- 将主方向投影回图像平面得到灭点;
- 连接灭点和线段$l_i$中点得到直线$l$;
- 如果$l_i$和$l$之间的重合误差不超过4个像素,则确定了$l_i$的主方向;
- 计算光心的投影点$O’$;
- 计算方向角 $\theta$,同时将逆深度$h$初始化为一个缺省值。
为简化计算,仅选择图像中的长线段;为了实现后续的线段匹配,保留线段中点11*11像素的图像patch。
Structure Line的观测模型
系统中使用LSD算法提取二维线段,整个观测模型中的关键部分有三点:
- Structure Line的数据关联算法;
- Structure Line投影到图像平面的方法;
- Structure Line的投影直线与二维观测线段间的误差计算公式。
由于Structure Line的数据关联算法涉及了EKF框架中的运算,将放到下一章系统结构中阐述。
Structure Line的投影
简要来说,SL(Structure Line)的投影等同于三维点的投影过程,当得到了SL定义中那个平面交点$A$在图像上的投影点之后,连接这个投影点和这条SL对应的图像灭点就可以得到投影直线,平面交点的投影过程如下:
- 将相机坐标系下的三维交点转换到世界坐标系下:$A^w=P^T([c_a,c_b]^T+(1/h)[\cos(\theta),\sin(\theta)]^T)$,此处$h$为逆深度,$P$为一个相机坐标系的投影矩阵(三维投影到二维,转置之后就可以计算三维点了),和之前SL的示意图对比,很容易理解,只是一个二维点+逆深度->三维点的过程。
- 将世界坐标系下的三维点投影到当前相机坐标系:$A^c=R^{cw}h(A^w-p^w)$,其中$p^w$是当前相机光心在世界坐标系下的坐标;
- 将$A^c$投影到当前平面,得到二维点$a^c$,两点(这个点与对应灭点$v$)确定一条直线$v \times a^c$,这条二维直线即为投影直线。
Structure Line的投影误差计算
使用基础的二维点线距离来计算:观测线段的端点+SL的投影直线。这里有两个trick:
- SL与图像平面中二维线段是一对多的关系;
- 为了让图像平面中的长线段为优化提供更多贡献,作者按照的30个像素的长度将长线段截断,即一条长线段现在拥有了$2*n$个端点($n$为截断得到的短线段条数),自然其观测误差就变大了。
第$i$条SL的观测误差为$m_i=(m_{i1},m_{i2},…),其中$第$i$条SL与第$j$个观测线段间的误差为$m_{ij}$。
EKF中的测量方程可以表示为:
\[h(x)=[m_1^T,...,m_i^T,...,p_1^T,...p_k^T,...]+R\]其中$R$表示测量噪声,而这个$p$在论文中表述为点的观测误差,并且引用了MonoSLAM的论文,所以这可能还是个点线结合的SLAM,但这部分作者并未详述。
StructSLAM系统结构
基于EKF,其量测方程为上述的$h(x)$,状态方程为:
\[\begin{equation} \begin{aligned} f(x) &= [x_c^T,x_p^T,x_l^T] = [g(x_c)^T,x_p^T,x_l^T] + Q \\ g(x_c) &= \begin{pmatrix} p^w+v^wt \\ q^{wc}q(w^c)t \\ v^w \\ w^c \end{pmatrix} \end{aligned} \end{equation}\]其中相机状态包括线速度、角速度、位置、方向四个量,假设符合匀速运动模型,$Q$为噪声。
预测过程(其中$F_x$、$F_Q$分别为$f(x)$ 对$x$和$Q$的雅克比矩阵,$\Sigma$和 $\Sigma_Q$分别为上一时刻系统的协方差矩阵和噪声的协方差矩阵):
\[\begin{equation} \begin{aligned} x_k &= f(x_{k-1}) \\ P_k &= F_x \Sigma F_x^T + F_Q \Sigma_Q F_Q^T \end{aligned} \end{equation}\]更新过程(其中$H$为$h(x)$ 的雅克比矩阵,$r$为观测残差):
- 卡尔曼增益: $K_k=P_kH_k^T(HP_kH^T+R)^{-1}$
- 状态更新: $\hat{x}_k = x_k + K_kr$
- 协方差更新:$\hat{P}_k = P_k-K_kH_kP_k$
介绍完了系统结构,可以给出SL的数据关联算法:
- 找到与SL匹配的二维线段候选集合,这部分采用几何距离的计算方法,距离$s=r_i^T(H_iH_i^T)r_i^T$,$H$和$r$上面已经介绍过了,如果$s<=5.99$,那么这条二维线段作为$i-th$ SL的候选关联线段;
- 每条SL对应一个11*11的patch,计算SL的patch和候选二维线段中心点的patch之间的ZNCC(Zero-based Normalized Cross Correlation),阈值为0.8;
- 现在得到了缩小的候选匹配集合,接着使用RANSAC方法进一步提出外点:
- 随机选择一条二维线段;
- 使用这个线段匹配对进行EKF更新;
- 计算更新后的SL与匹配线段的距离,阈值以内的当做内点。
Experiments
在RAWSEEDS 2009数据集上的实验结果:

运行时间:在Biccoca 2009-02-27a场景中,平均运行时间25.8ms/帧,最大运行时间62.9ms/帧 (限制每帧特征点数目为40,每个方向的SL线段最多8条,共24条)。运行时间会随着系统的连续运行而增大。
Conclusion
StructSLAM利用了场景中存在的全局约束来优化SLAM运行结果,由于这个约束较强,效果(尤其是建图效果)很惊艳,另外一个很突出的优势就是在没有使用闭环检测的情况下位姿基本不会出现大的漂移,三个全局主方向规整了整个运行轨迹和地图。
使用EKF框架导致系统在大规模场景中的性能存疑,例如实验过程中考虑到系统的实时运行将每帧最大特征数目限制为64(点+线),这对整个系统的鲁棒性提出了考验。
转载请注明原地址,魏鑫燏的博客: http://slowlythinking.github.io 谢谢!





