论文
《StructVIO : Visual-inertial Odometry with Structural Regularity of Man-made Environments》(2019IEEE Trans on Robotics, Shanghai Jiao Tong University)
Open Source
项目主页(提供了数据集和二进制运行库的下载)
BackGround
Atlanta World Model
Atlanta World:包含多个曼哈顿世界假设的场景,即全局中包含多个曼哈顿场景,这些场景均具有三个互相垂直的主方向,不过各场景之间的主方向不同向。
来自论文《Atlanta world: An expectation maximization framework for simultaneous low-level edge grouping and camera calibration in complex man-made environments》(ICCV&PR 2004)
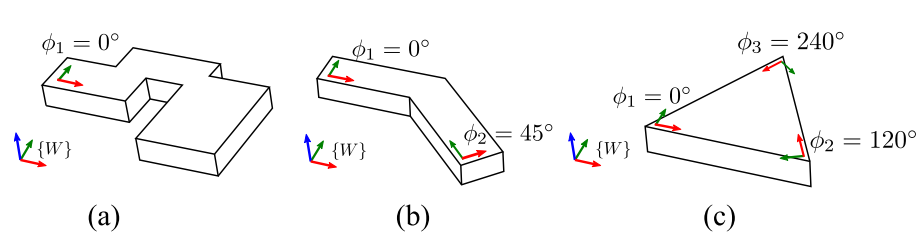
StructVIO中不要求单个曼哈顿场景必须能检测出三个主方向,仅检测出一条水平方向主方向时,也认为这是一个曼哈顿场景。如下图,其中a为曼哈顿世界假设,b、c为Atlanta世界假设,可以看到Atlanta假设中不需要局部的Manhattan场景具有完备的三个方向,最低有一个不同的水平方向即可(实际上论文中的局部Manhattan场景均具有相同方向的z轴——重力方向的反方向,它们之间不同的也只有水平方向夹角这一个量)
vSLAM / VIO中线特征的问题和相关工作
- 相比于线,点特征是一种普遍存在、在大多数场景中都能找到的特征;
- 相比于线,点特征的检测和跟踪工作更加成熟;
- 相比于线的的5DoF(论文中表述如此,正确应为4),3DoF的点更易初始化(尤其是角度部分)和优化。
- 有一些工作使用图像灭点,灭点一般是由图像中的平行线得到的,他们仅使用了灭点而没有使用线特征,相关工作:
- “Vpass: Algorithmic compass using vanishing points in indoor environments,” in IEEE/RSJ Proc. of Intelligent Robots and Systems. IEEE, 2009.
- “Loop closure through vanishing points in a line-based monocular slam,” in Proc. IEEE Int. Conf. Robotics and Automation. IEEE, 2012
- “Using vanishing points to improve visual-inertial odometry,” in Robotics and Automation (ICRA), 2015
- 线特征VIO:
- “Exploiting urban scenes for vision-aided inertial navigation.” in Robotics: Science and Systems”, 2013
Motivation
- 大多数vSLAM系统关注通用场景,而在人造场景这类特殊场景中,存在着较强的结构规整性,例如在曼哈顿世界假设下,垂直方向的平面和直线就占了主要部分。
- 已经有一些vSLAM、场景三维建模、场景理解工作使用了这样特殊场景下的结构规整性,并且提高了系统的精度和鲁棒性;
- 曼哈顿场景存在局限性,扩展之后的Atlanta World能够解决这个问题。
- 在VIO中利用环境的结构规整性是很合适的:IMU提供了重力方向信息,即使图像中只有重力方向的垂直线段,也能对翻滚角和俯仰角进行有效约束。
Contribution
- 提出了一个新的线特征表示方法,这个表示法中集成了Atlanta世界假设和人造建筑物的结构特征;
- 算法较为鲁棒:SL(Structure Line)和局部曼哈顿场景都是在线识别的;没有SL的时候系统为一个纯粹的点特征SLMA;没有监测到局部曼哈顿场景+仅有垂直线段时系统也能利用垂直线段进行优化;
- 在线特征处理方面的贡献:新的直线跟踪算法;新的直线跟踪的边缘化算法。
Content
局部Manhattan场景的检测和融合
这部分是StructSLAM与StructVIO的不同之处:存在多个局部M场景,而且包含了IMU信息(主要使用重力方向信息)。具体来说,由于已知重力方向,就可以将世界坐标系的Z轴设置为与重力方向共线,那么此时将世界坐标系中XY平面投影到图像平面,就可以得到一条灭线(vanishing line) $l_{van}$ ,全部X、Y方向的灭点都在这条线上。由此可以用RANSAC算法来处理。
- $l_{van}$ 的计算:
- RANSAC算法流程:
- 随机选取一条二维线段;
- 将线段延长,与 $l_{van}$ 相交于 $v_{x}$ ,此点为灭点,假设它为新的局部M场景的X轴方向。
- 已知 $v_{x}$ 和重力方向,把这个局部M场景的坐标系计算完整;
- 计算图像中符合上述局部M场景假设中X、Y轴的SL线段数目;
- 如果数目大于4 且 数目大于图像中已知的SL,得到了新的局部M场景,否则返回1.
融合部分比较容易,两个局部M场景的X/Y轴夹角小于5度,融合为一个,一般是将新生成的融合进老的M场景。
注意:仅当图像中检测出了重力方向的SL时(参见下面的SL的初始化),才开始局部M场景的检测。
SL的参数化
粗略来说,StructVIO中有两类SL:与重力方向(Z轴)共向的、与XY平面重合的。前者直接在世界坐标系下建模,后者在局部M场景下建模。
在不同参数空间中,SL有不同表示,这里的参数空间有:
- {L} : 局部Manhattan场景三个主方向平面,与{S}的转换由旋转矩阵 $R_L^S$ 完成,下图中包含蓝色平面的部分;
- {S} : 初始观测到该SL的帧坐标,这个坐标是经过旋转处理过的,与局部Manhattan场景或者世界坐标系中的主方向同向,可以视为局部M场景坐标系(旋转矩阵相同位移向量不同)。
- {C} : 其他观测到该SL的帧坐标空间。
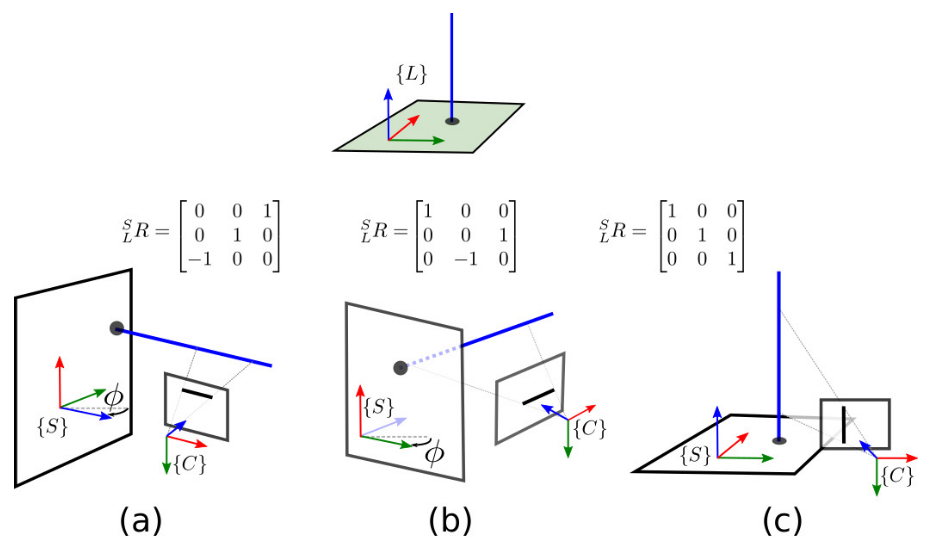
SL的参数表示:
- 在{L}参数空间中,SL表示为其与最匹配的局部M场景主方向为法向量的平面的交点 $p_l=(a,b,0)^T$ (注意此处可以看作是一个XYZ轴数值顺序未确定的局部M坐标系下的三维点),也可以用角度和逆深度表示 $p_l = (\theta, \rho, 0)^T$ ,其中: $\theta = atan2(a,b), \rho = 1/\sqrt{a^2+b^2}$。这部分坐标系相关的信息文中未明确说明,但从StructSLAM及后续L到S的转换来看,应为如此
- 在{S}参数空间中,SL依然表示为一个三维交点,只不过从{L}转换到了{S},其实就是将SL与对应主方向平面的交点转换到正确的局部M坐标系下,这里的转换有三种情况:SL与局部Manhattan场景中同向的主方向分别是X、Y、Z轴时。具体计算过程对应上图中的三个矩阵:
- 在{W}参数空间中,将以上交点转换到世界坐标系下就可以了,如果{S}参数空间是与局部Manhattan场景主方向同向,则使用旋转矩阵 $R(\phi_i)$ + 世界坐标系下的相机光心 $p_s^W$ 来进行旋转变化,这里的 $\phi_i$ 表示第$i$个局部M场景,具体来说表示这个场景的水平角度,由于全部局部场景z轴同向,所以 $\phi_i$ 可以唯一地确定这个局部场景。如果{S}参数空间是与世界坐标系主方向同向,不需旋转变换,只需平移变换。
总结:对于一个SL特征,可以使用如下参数唯一确定:
- 它属于哪个局部M(即 $phi_i$);
- 它对应局部M中的那个主方向 (即矩阵 $R_L^S$);
- 它与所在局部M坐标系中,以其主方向为法向量的平面的交点 (即 $(a,b)$)。
SL的投影
SL投影到二维图像平面与StructSLAM中的操作类似,同时将SL的线面交点、SL对应的主方向投影到图像平面,得到投影点和图像灭点。
这里描述下灭点的投影过程,如果是与重力方向对应的灭点:
\[\begin{equation} v_z=KR_W^C\begin{bmatrix} 0 & 0 & 1 \end{bmatrix}^T \end{equation}\]第 $i$ 个局部Manhattan场景(水平方向与世界坐标系夹角为 $\phi_i$ )中X轴方向的灭点:
\[\begin{equation} v_x=KR_W^C\begin{bmatrix} \cos{\phi_i} & -\sin{\phi_i} & 0 \end{bmatrix}^T \end{equation}\]第 $i$ 个局部Manhattan场景中Y轴方向的灭点:
\[\begin{equation} v_y=KR_W^C\begin{bmatrix} \sin{\phi_i} & \cos{\phi_i} & 0 \end{bmatrix}^T \end{equation}\]SL的跟踪
使用LSD算法提取图像中的二维线段。
在以上参数化的基础上,定义SL的端点为 $p_l^s=(a,b,r_s)^T$ , $p_l^e=(a,b,r_e)^T$ (在{L}参数空间中) ,新加入的变量 $(r_s,r_e)$ 表示端点在{L}中的z轴值(这里有个问题,按这个表达式,这两个“端点”不一定在直线上,可能这里只是为了简化表达, $(a,b)$ 应为 $(a’,b’)$)。
3D SL - 2D line 匹配:
- 将SL投影到图像平面;
- 通过投影直线与平面内线段的角度、位置距离缩小候选匹配集合;
- 基于图像点周围patch间的ZNCC(zero mean normalized cross-correlation)来确定最优匹配,这里与StructSLAM不同的是这里等距取了多个采样点(这也是前面要加个端点的原因),如下图:
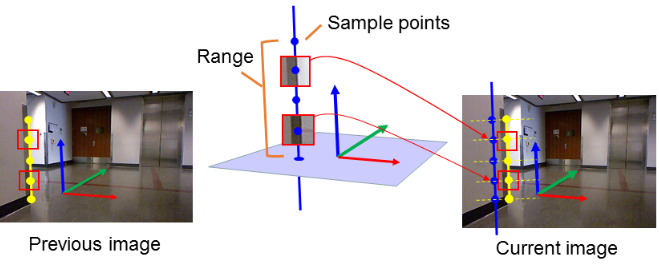
注意:在StructSLAM中匹配过程是一对多的形式,在StructVIO中似乎是一对一。
SL的初始化
首先是识别图像中的SL,与StructSLAM中做法一致:计算灭点,连接线段中点与灭点,计算两条线段的重合程度。不同之处:这里有多个局部M场景,就有多个XY轴方向的灭点,而StructSLAM中最多只有三个灭点。
然后是对这些识别出的SL进行选择,按以下标准:
- 长线段
- 距离已经初始化的SL比较远的线段
最后对选择的SL进行初始化(事实上是一个迭代过程:选择-初始化-选择-…,这里为描述方便,简化):
- 为SL建立{S}(即Start Frame),如果是重力方向(Z轴)的SL,则{S}={W};
- SL中三维交点的参数为 $(\theta,\rho)$,其中逆深度 $\rho$ 初始化为缺省值, $\theta$ 则使用直线 $l_{temp}$ 与X/Y轴夹角来近似,其中直线为{S}光心与二维线段上中点 $m$ 的连线。对于XY平面的SL:
系统结构
StructVIO基于EKF,使用了与MSCKF《A multi-state constraint kalman filter for vision-aided inertial navigation》(2007ICRA)相同的滤波框架:系统状态中包含多帧信息,同时所有点线特征仅用于计算IMU位姿之间的几何约束,不参与滤波过程。
系统状态:
\[x_k=[x_{I_k}, \tau_C^I, \phi_i,...,\phi_N,\tau_{I_1}^W,..., \tau_{I_M}^W]\]其中:
- $x_{I_k}$ : k时刻的IMU状态,包括位姿、速度、加速度计和陀螺仪的bias。
- $\tau_C^I$ : IMU与相机之间的相对位姿关系
- $\phi_i,…,\phi_N$ : N个局部M场景的X/Y轴角度
- $\tau_{I_1}^W,…, \tau_{I_M}^W$ : 第1~M时刻IMU的位姿(历史信息)。
预测:
- 系统状态。此处使用IMU积分(Runge-Kuatta 方法,由 $\varrho(·)$ 函数表示)来预测k时刻IMU的位姿,其中 $\omega_{k,k-1}$ 和 $a_{k,k-1}$ 分别表示k-1到k时刻之间的陀螺仪和加速度计信息。
- 协方差矩阵。这部分与标准EKF没什么不同,公式推导略过。
注意:系统状态中不包含SL,那么SL是怎么更新的?由于SL与局部M环境中的主方向直接相关,而系统状态中是包含局部M环境主方向( $\phi_i$ )的,在接下来的更新过程会得到更新,因此SL也会更新
更新:
系统状态和协方差矩阵的更新也遵循标准EKF流程,略过,这里重点关注几个特殊的点:
- 测量方程中SL的误差由点线距离表示(同StructSLAM);
- 系统中全部雅克比矩阵的计算均采用数值微分(numerical differentiation)的方法,而没有进行公式推导。
- EKF的更新时机:
- 当系统对几帧位姿不能恢复时进行更新,而不是在SL没有被当前帧观测时更新,作者认为SL特征可能在某些帧短暂地丢失,如果此时进行更新,全部与此SL相关的历史位姿均需要更新,计算负载过大,作者称这个feature为“延迟更新策略”
- 系统状态内位姿数目超过了最大值。
Experiments
在EuRoC上,最大特征数目设置为:125个点,30条SL。实验结果(其中对比的是没有闭环检测模块的VINS):
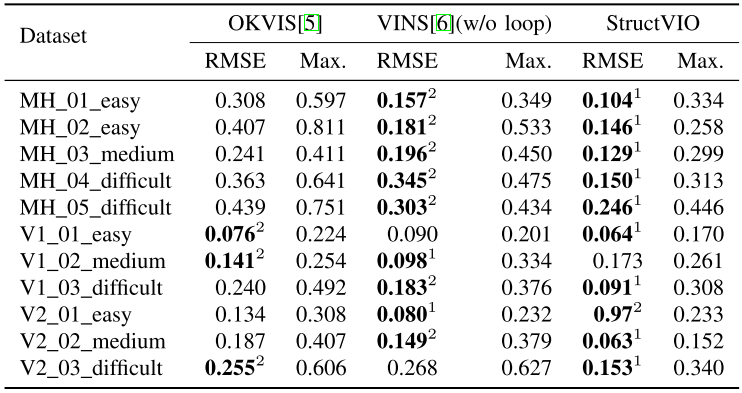
以下为VINS-mono论文中的实验结果:
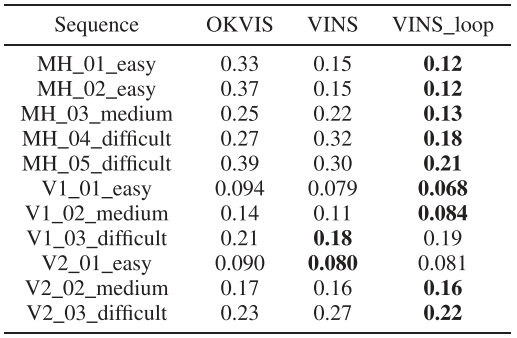
同时作者分析了不同场景下基于点+EKF的VIO、基于点线+EKF的VIO(前面两个都是作者自己实现的、不包含Manhattan场景假设的EKFSLAM)和StructVIO的性能,说明了结构规整性强的Machine hall场景中StructVIO优势明显。
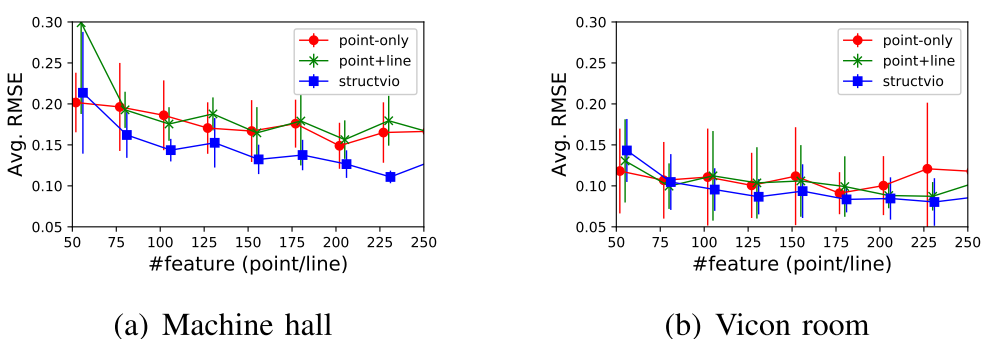
在作者提出的数据集上进行的实验,运行速度为15帧/s,作者认为运算时间的瓶颈在于SL的提取和跟踪部分,位姿轨迹误差如下:
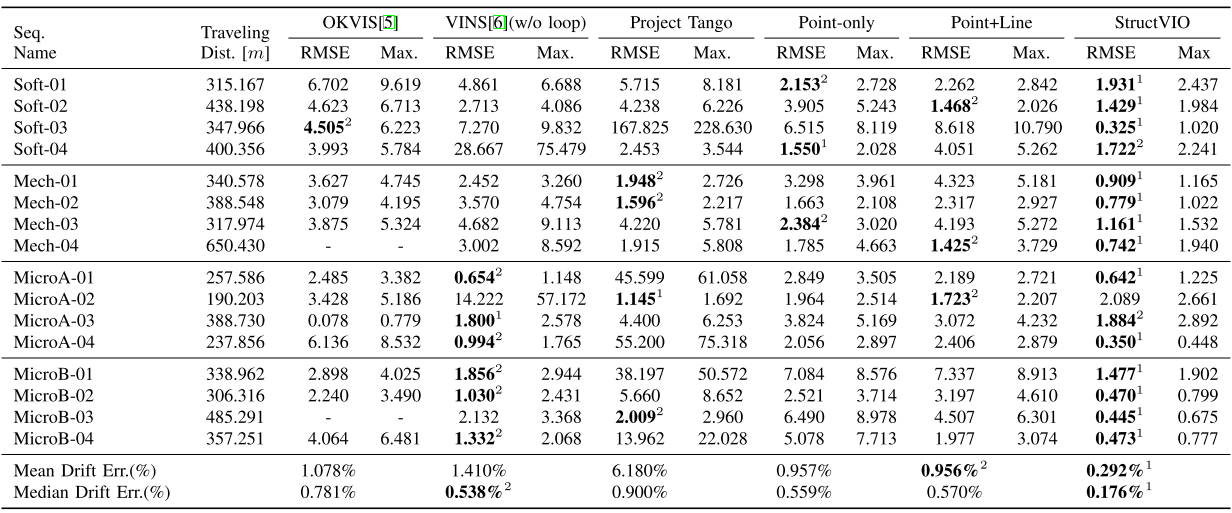
同时作者也给出了在这个数据集上,使用Manhattan世界假设和Atlanta世界假设时的位姿轨迹误差,可以明显看出RMSE的较大差异。
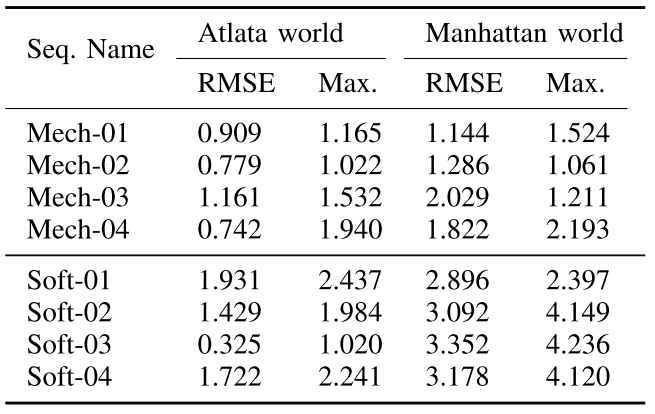
Conclusion
这份工作是对StructSLAM的扩展,扩展了结构规整性的假设、扩展了传感器的类型(IMU)。属于系统性的创新,至于可借鉴的部分,有以下几点:
- IMU提供的重力方向在结构规整性假设中的价值很大;
- 结构规整性检测可以使用灭点和灭线+RANSAC算法来完成;
- 结构规整性在算法中的表现形式,最好用新特征参数来实现,而非加在优化过程;
- EKF的更新过程可以推迟;
转载请注明原地址,魏鑫燏的博客: http://slowlythinking.github.io 谢谢!





