论文

《Monocular Visual Odometry Initialization with Points and Line Segments》(2019IEEEAccess, National University of Defense Technology, China)

Open Source

None.

BackGround

SLAM/VO系统的初始化问题可以看作是一个特殊的SFM（Structure From Motion）问题：即在较小的运动过程中恢复三维结构，近期SfSM（Structure from Small/accidental Motion）被提出，SfSM关注短基线运动下的结构恢复，同时SfSM不只使用两帧数据。

SLAM/VO中的初始化过程

目前在SLAM/VO中常用的初始化方法可以分为矩阵分解和随机深度初始化两类：

1. 随机深度初始化：将第一帧像素点的深度初始化为一个随机产生的值（一个方差很大的分布），通过之后多个关键帧的观测来将这个随机深度值约束到一个收敛值。使用这一方法的相关论文：
   • 《Lsd-slam: Large-scale direct monoc- ular slam》（2014ECCV）
   • 《Dpptam: Dense piecewise planar tracking and mapping from a monocular sequence》（2015IROS）
2. 矩阵分解：包括本质矩阵分解和单应矩阵分解两类，其中后者假设场景是一个共面的二维场景（DTAM和SVO使用这一方法），ORB-SLAM2同时使用了这两个分解方法，最后使用一个阈值来判断使用哪一个方法的结果。使用本质矩阵分解的论文：
   • 《Dt-slam: Deferred triangulation for robust slam》（2014 3DV）
3. 在2004年《多视几何》中，基于两帧的重建描述为以下三个步骤：
   • 从二维点匹配对中计算基础矩阵；
   • 基于基础矩阵计算相机矩阵；
   • 对于每一个点匹配对，计算三维点。

SfSM相关的研究

• 《A closed-form solution to rotation estimation for structure from small motion》（IEEE Signal Processing Letters 2017）；[32]
• 《High quality structure from small motion for rolling shutter cameras》（ICCV2015）；[29]
• 《High-quality depth from uncalibrated small motion clip》（CVPR2016）[28]

已有的这些SfSM的工作都是基于点特征的，虽然线特征在人造场景中很常见，但是线特征存在较为严重的退化（degeneracy）问题，尤其是在短基线运动的场景下。

一般在SfSM相关研究中，存在两个假设：

1. 相比于场景的深度值，相机的平移运动是足够小的；
2. 能够使用一阶泰勒展开来近似表示相机运动中的旋转矩阵。

第二个假设的数学表达： $i$-th相机的旋转矩阵可以近似表达为：

其中 $\lbrack r_i \rbrack_{\times}$表示旋转向量 $r_i=(r_i^x,r_i^y,r_i^z)$的斜对称矩阵。虽然此处：

但在微小运动的情况下可以使用。来自论文《3d reconstruction from accidental motion》（2014CVPR）[31]。

线特征重建的退化问题

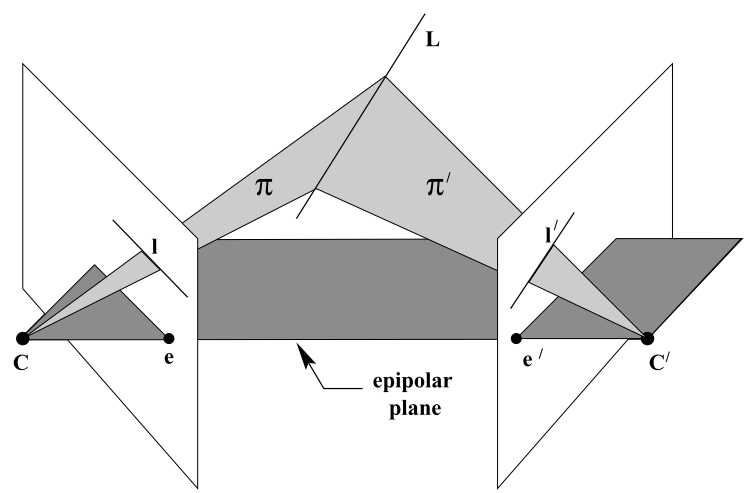
在2004《多视几何》中对这一问题的描述：

Degeneracy. As illustrated in figure 12.8 lines in 3-space lying on epipolar planes cannot be determined from their images in two views. Such lines intersect the cam- era baseline. In practice, when there is measurement error, lines which are close to intersecting the baseline can be poorly localized in a reconstruction. The degeneracy for lines is far more severe than for points: in the case of points there is a one-parameter family of points on the baseline which cannot be recovered. For lines there is a three-parameter family: one parameter for position on the baseline, and the other two for the star of lines through each point on the baseline.

在实际操作中，靠近极线的线段重建时，错误的线段匹配也可能计算出很小的投影误差。三维直线的重建退化问题比点严重，因为只有一类点无法重建：和极点重合的，但是对于线来说却有多种不能重建的情况（在对极平面以内的都不能重建），即one-parameter family of points和three-parameter family of lines不能重建。

线特征重建退化问题的解决方案

1. 当线段靠近极线时使用人工构造的点来辅助进行三维线段重建，相关论文：
   • 《Accurate reconstruction of near-epipolar line segments from stereo aerial images》（2012 PFG）[33]
   • 《Visual localization with lines》（2017 PHD dissertation, University of Heidelberg）[34]
2. 使用重建线段到基线的距离来剔除退化情况，相关论文：
   • 《3d surface reconstruction from point-and-line cloud》（2015 3DV）[35]

Motivation

1. 线特征在人造场景中较为丰富，已经被一些学者用到了SLAM/VO中。
2. SLAM/VO的初始化是一个基于短基线运动的SFM问题，在短基线运动中，图像内容更容易受旋转运动影响而变化（而非平移运动），而旋转运动与线特征之间存在紧密的关联。
3. 线特征初始化目前存在相对点特征更为严重的退化问题。
4. 目前已经有一些SfSM领域的工作，它们致力于解决短基线运动情况下的重建工作，这是可以借鉴到SLAM/VO初始化过程的。

Contribution

1. 提出了一个联合点线特征的初始化算法；
2. 提出了一个在短基线运动中基于线特征的旋转分析算法，形式：闭式表达式（closed-form expression）；
3. 提出了一个经过数学证明的退化线段剔除标准。

Content

主要流程

1. 获取初始化所需的帧队列，以及其中的点线特征匹配对，这其中的主要工作在于线特征匹配；
2. 使用线特征匹配对计算各帧与参考帧之间的旋转矩阵。
3. 使用基于Plucker表示的三维线特征的约束来优化第二步得到的旋转矩阵；
4. 固定旋转矩阵，联合点线的投影误差函数来优化平移向量及三维特征深度信息。
5. 联合优化旋转矩阵（近似表达形式）、平移向量等参数。
6. 丢弃之前使用的旋转矩阵的近似表示，联合优化旋转矩阵、平移向量等参数。

1.特征跟踪及初始化帧的选择

点特征

使用跟踪点视差中值（The disparity medians of the point features tracked between the new frame and all frames）。

设置两个阈值： $\tau_{dmin}$ 和 $\tau_{dmax}$，当当前帧与参考帧之间的跟踪点视差中值超过 $\tau_{dmin}$ 时，将当前帧加入初始化帧序列，如果超过了 $\tau_{dmax}$，并且存在帧队列中存在超过三帧以上的帧，将当前帧加入初始化帧序列并开始初始化。如果 $\tau_{dmin}$ 越小，或者 $\tau_{dmax}$ 越大，则跟踪点越少、队列中的帧越多。

线特征

使用三个约束来完成线特征匹配/跟踪：

1. 几何约束：其中$a$、$b$、$c$分别为两个跟踪线段之间端点的距离以及原线段本身的长度，此处使用光流跟踪线段端点。 \(\begin{equation} s_g = \begin{cases} 1-4ab/c^2,& a/c\leqslant0.25 \&\& b/c\leqslant0.25; \\ 0,& a/c>0.25 \&\& b/c>0.25. \end{cases} \end{equation}\)
2. 对极约束：其中蓝色线段为当前帧内二维线段所在直线，虚线为参考帧中对应线段端点的极线。
   • \[s_e=\frac{AB}{CD}\]
   • 
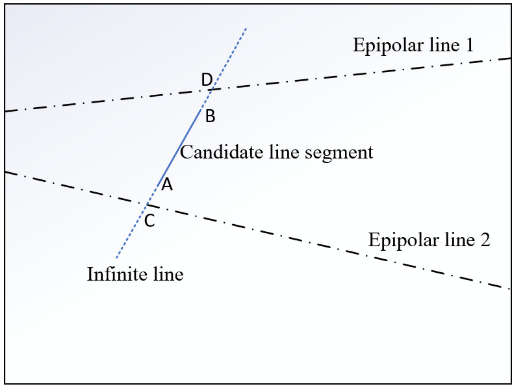
3. 描述子距离：使用LBD描述子，计算两条线段描述子之间的汉明距离。 \(\begin{equation} s_d = \begin{cases} 1,& d_H(D_r,D_c)< \tau_{des}; \\ 0,& d_H(D_r,D_c)\geqslant \tau_{des}. \end{cases} \end{equation}\)

最终分数为 $s=s_gs_es_d$

2.基于线特征匹配对的旋转分析

使用的约束：三维线段的端点投影到当前帧，得到两个二维点，当前帧内与该三维线段匹配的二维线段所在的直线为$l$，这两个点在$l$上。

• 三维线段的投影。使用端点投影:$x_{rep}^s=\pi(R_{i}x_{0k}/\omega_{ks}+t_i)$，其中 $\pi$表示将二维点坐标表示为三维齐次坐标，$\omega$表示点的反向深度；
• 由二维线段的两个端点得到共线直线：$l_{ik}=x_{ik}^s \times x_{ik}^e=(a_{ik},b_{ik},c_{ik})$；
• 共线约束：$l_{ik}^Tx_{rep}^s=0$

最终得到的目标函数公式： \(Ar_i^x+Br_i^y+Cr_i^z+D=0\)

计算可得：$A,B,C,D$四个参数中，仅有参数D包含平移向量$t_i$和反向深度 $\omega_{ks}$，但由于是微小运动（参见前面的假设），此处可近似地丢弃平移向量和反向深度项： \(D=l_{ik}^T(x_{0k}^s+ \omega_{ks}t_i)\) \(D\approx l_{ik}^Tx_{0k}^s\)

使用上述目标函数公式，利用SVD分解和RANSAC算法来求出旋转矩阵的三个参数 $(r_i^x,r_i^y,r_i^z)$。

3.旋转矩阵的优化

使用Plucker坐标表示三维线段 $(m_{ik},d_{ik})$，其中参数分别为线矩和线方向，线方向的长度为1一个单位长度。可得以下约束（其中$n_k^i$是一个与$m_{ik}$ 同向的向量，可以由二维线段的两个端点计算得到）： \((R_id_{0k})^Tn_k^i=0\)

最小化以上函数可以同时优化旋转矩阵和三维直线Plucker坐标中的线方向$d_{ik}$。

4.固定旋转矩阵，联合优化平移向量、特征反向深度和三维线段参数

联合点线特征的投影误差，优化标题中的变量。其中点特征误差为投影点与匹配点的距离，线特征误差为投影端点与匹配线段所在直线的点线距离。

5.联合优化旋转矩阵、平移向量、特征反向深度和三维线段参数

联合优化标题中的变量。其中旋转矩阵为前述近似表示形式。

6.联合优化旋转矩阵、平移向量、特征反向深度和三维线段参数

联合优化标题中的变量。其中旋转矩阵为$SO(3)$形式。作者此处说明：

$R_i$ is orthogonalized and scaled to initialize $R_{ic}$

但不太清楚具体怎样初始化这个$SO(3)$形式的$R_{ic}$。

Experiments

作者使用了ICL-NUIM数据集（一个人造数据集，包含相机位姿和环境点云的Ground Truth）和实地运行两个测试方案。

位姿精度（其中平移向量只算角度误差，因为尺度未知）

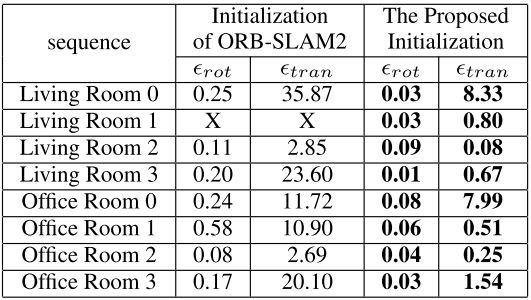
建图精度（其中$N_p$为5次运行生成的三维点数目，$r_g$为好的三维特征的比例）

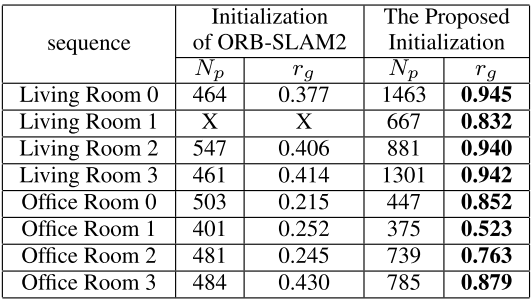
Conclusion

这份工作主要是对论文《A closed-form solution to rotation estimation for structure from small motion》（2017 SPL）的一个扩展。个人觉得属于琐碎、难以验证的创新，这类工作中可能一到两个细节就会决定整个方案的性能，而没有公布开源代码的情况下很难follow。

不过文章中线特征匹配的方法感觉有一定借鉴意义，三重约束可能会提高匹配的准确性，对于地图重建和位姿计算方面，其中的部分公式推导的工作量感觉不算小。

转载请注明原地址，魏鑫燏的博客： http://slowlythinking.github.io 谢谢！